AdaBoost (Adaptive Boosting) is one of the most popular machine learning algorithms for boosting. It builds a strong classifier by combining multiple weak classifiers, typically decision stumps (shallow decision trees). This post will provide an in-depth understanding of AdaBoost, including its geometric intuition, step-by-step working, implementation from scratch, hyperparameter tuning, and a comparison with bagging techniques.
Geometric Intuition
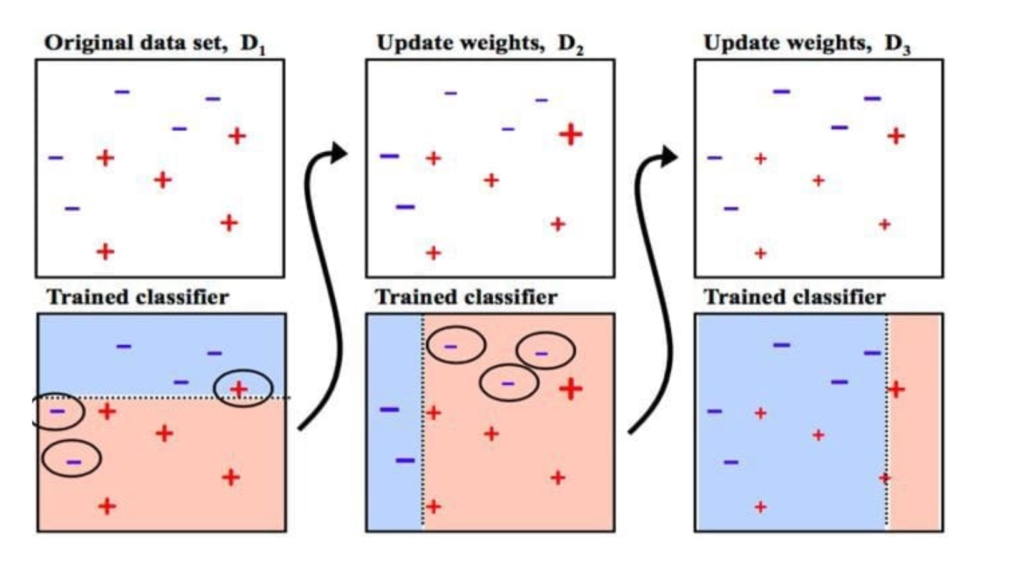
To grasp AdaBoost intuitively, imagine separating two classes in a dataset using straight lines (decision boundaries). A single weak classifier may fail to find a perfect separation. AdaBoost combines multiple weak classifiers to create a strong decision boundary.
Here’s how it works geometrically:
Weighted Focus: It assigns weights to each data point. Misclassified points are given higher weights to ensure subsequent classifiers focus on these difficult examples.
Cumulative Boundary Improvement: Weak classifiers iteratively refine the decision boundary. The final decision boundary is a weighted combination of all weak classifiers, achieving superior separation.
Margin Maximization: It increases the margin between classes, making the model robust to noise and outliers.
Algorithm: Step-by-Step Explanation
1. Initialize Weights
Each data point is assigned an equal weight, , where is the number of samples.
2. Train Weak Classifier
A weak classifier (e.g., a decision stump) is trained using the weighted dataset.
3. Calculate Classifier Error
Compute the error rate, , where:
is an indicator function.
is the prediction of the weak classifier.
4. Compute Classifier Weight
The weight of the weak classifier is calculated as:
5. Update Sample Weights
Update the weights for the next iteration: Normalize the weights so that they sum to 1.
6. Combine Classifiers
The final classifier is a weighted sum of all weak classifiers:
7. Repeat
Steps 2 to 5 are repeated for a specified number of iterations or until the error rate reaches zero.
Implementation: Code from Scratch
Here is a Python implementation of AdaBoost:
import numpy as np
class AdaBoost:
def __init__(self, n_estimators):
self.n_estimators = n_estimators
self.alphas = []
self.models = []
def fit(self, X, y):
n_samples, n_features = X.shape
weights = np.ones(n_samples) / n_samples
for _ in range(self.n_estimators):
stump = self._train_stump(X, y, weights)
predictions = stump['predictions']
error = np.sum(weights * (predictions != y))
alpha = 0.5 * np.log((1 - error) / (error + 1e-10))
weights *= np.exp(-alpha * y * predictions)
weights /= np.sum(weights)
self.models.append(stump)
self.alphas.append(alpha)
def predict(self, X):
final_prediction = np.zeros(X.shape[0])
for alpha, model in zip(self.alphas, self.models):
final_prediction += alpha * model['predictions']
return np.sign(final_prediction)
def _train_stump(self, X, y, weights):
n_samples, n_features = X.shape
min_error = float('inf')
stump = {}
for feature in range(n_features):
thresholds = np.unique(X[:, feature])
for threshold in thresholds:
for polarity in [-1, 1]:
predictions = np.ones(n_samples)
predictions[polarity * X[:, feature] < polarity * threshold] = -1
error = np.sum(weights * (predictions != y))
if error < min_error:
min_error = error
stump['feature'] = feature
stump['threshold'] = threshold
stump['polarity'] = polarity
stump['predictions'] = predictions
return stumpHyperparameters | GridSearchCV in AdaBoost
It has several hyperparameters that can be optimized:
n_estimators: Number of weak classifiers.
learning_rate: Shrinks the contribution of each weak classifier.
Here is how to use GridSearchCV:
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import GridSearchCV
# Define parameter grid
param_grid = {
'n_estimators': [50, 100, 150],
'learning_rate': [0.01, 0.1, 1]
}
# Initialize AdaBoost
model = AdaBoostClassifier()
# Perform GridSearch
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5)
grid_search.fit(X_train, y_train)
# Best parameters
print("Best parameters:", grid_search.best_params_)Bagging Vs Boosting | What is the Difference?
| Feature | Bagging | Boosting |
|---|---|---|
| Definition | Combines independent models. | Sequentially combines models. |
| Focus | Reduces variance. | Reduces bias. |
| Weighting | Equal weighting. | Adaptive weighting. |
| Training Style | Parallel. | Sequential. |
| Example | Random Forest. | AdaBoost, Gradient Boosting. |
Summary
Bagging stabilizes predictions by aggregating diverse models.
Boosting corrects errors by focusing on misclassified samples.
It is a versatile and powerful algorithm for classification tasks. While it is sensitive to noise, proper hyperparameter tuning can enhance its performance. By combining weak classifiers adaptively, it demonstrates the strength of boosting techniques in achieving high accuracy and robustness.
FAQs
1. What is the primary advantage of AdaBoost?
It excels in converting weak learners into a strong classifier by iteratively focusing on difficult-to-classify samples. This adaptability allows it to handle complex datasets effectively.
2. What type of weak learners does AdaBoost use?
Typically, AdaBoost uses decision stumps (single-split decision trees) as weak learners. However, other simple classifiers can also be used.
3. How does it handle misclassified samples?
AdaBoost assigns higher weights to misclassified samples, forcing subsequent weak learners to focus more on these challenging points.
4. Can it handle noisy datasets?
While AdaBoost is robust to some noise, excessive noise can lead to overfitting as the algorithm emphasizes misclassified points, including noisy or outlier data.
5. What are the main hyperparameters to tune in AdaBoost?
Key hyperparameters include:
n_estimators: The number of weak learners in the ensemble.learning_rate: Controls the contribution of each weak learner.base_estimator: Specifies the weak learner type.