Random Forest Unleash Transformative Power ML in 6 steps

Ensemble learning is a powerful concept in machine learning that involves combining multiple models to achieve better predictive performance than a single model. By leveraging the strengths of individual models, ensemble techniques can improve accuracy, reduce variance, and enhance generalization. One of the most popular ensemble methods is the Random Forest algorithm.

Random Forest, developed by Leo Breiman, is an ensemble method that builds multiple decision trees and combines their outputs to make predictions. This blog will explore the intuition behind Random Forest, its performance, hyperparameter tuning, and other key concepts to provide a comprehensive understanding of this algorithm.

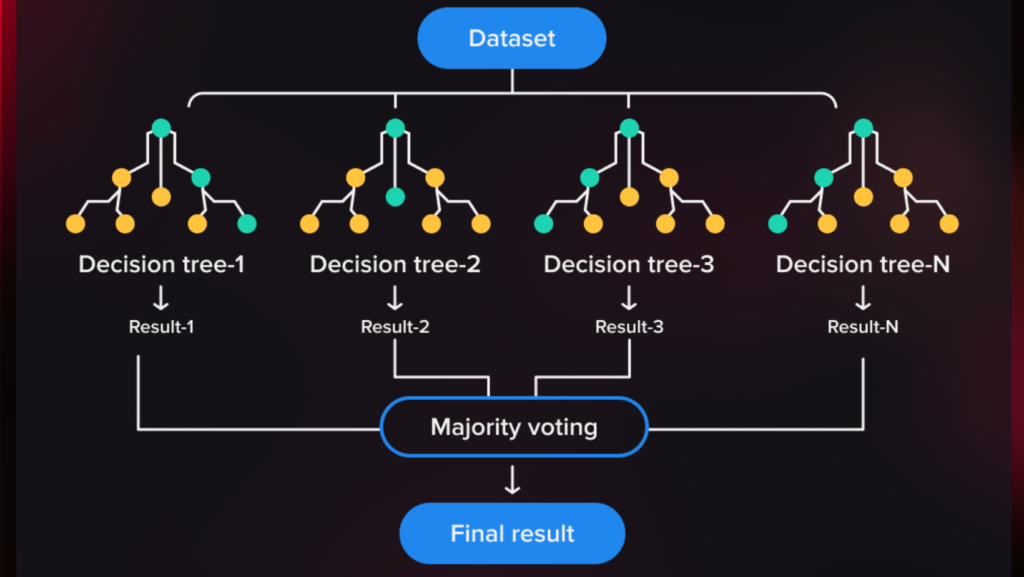
Ensemble Techniques in Machine Learning

Ensemble techniques can be broadly categorized into:

Bagging (Bootstrap Aggregating):
- It creates multiple subsets of the training data by sampling with replacement (bootstrap sampling).
- Each subset is used to train a separate model, and the predictions are aggregated (e.g., majority voting for classification or averaging for regression).
- Example: Random Forest.
Boosting:
- It builds models sequentially, where each subsequent model focuses on correcting the errors of the previous one.
- Example: Gradient Boosting, AdaBoost, and XGBoost.
Stacking:
- It combines multiple models using a meta-model, which learns from the predictions of the base models.

Random Forest falls under the Bagging category, where the focus is on reducing variance by combining independent decision trees.

Intuition Behind Random Forest

It is operates by constructing a “forest” of decision trees during training. Each tree is built using a random subset of the data and a random subset of features. The key steps include:

Bootstrap Sampling:
- A random subset of the training data is selected with replacement.
Feature Selection:
- At each split in the decision tree, a random subset of features is considered instead of all features.
Aggregation:
- Predictions from all trees are combined through majority voting (classification) or averaging (regression).

This randomness ensures that individual trees are uncorrelated, leading to better generalization and reduced overfitting.

Why Does Random Forest Perform So Well? Bias-Variance Trade-Off

The performance of it can be attributed to its ability to strike a balance between bias and variance:

Low Bias:
- Decision trees have low bias as they can capture complex patterns in the data.
Reduced Variance:
- Combining multiple uncorrelated trees reduces the overall variance of the model.
Robustness to Overfitting:
- By averaging predictions, Random Forest minimizes the risk of overfitting, especially when the number of trees is large.
Handling Missing Data:
- Random Forest can handle missing values effectively by using surrogate splits

Bagging vs Random Forest

Bagging and Random Forest share similarities but differ in a key aspect:

Bagging:
- Creates multiple models using bootstrap sampling but considers all features for splitting.
Random Forest:
- Adds an additional layer of randomness by selecting a subset of features at each split, making the trees more diverse.

Key Difference: The feature selection step in Random Forest reduces correlation among trees, improving its generalization performance compared to Bagging.

Random Forest Hyperparameters

Tuning the hyperparameters of Random Forest is crucial for optimizing its performance. The key hyperparameters include:

Number of Trees (n_estimators):
- Determines the number of decision trees in the forest. More trees generally improve performance but increase computation time.
Maximum Depth (max_depth):
- Limits the depth of each tree to prevent overfitting.
Minimum Samples Split (min_samples_split):
- The minimum number of samples required to split an internal node.
Minimum Samples Leaf (min_samples_leaf):
- The minimum number of samples required to be at a leaf node.
Maximum Features (max_features):
- The number of features to consider when looking for the best split.
Bootstrap:
- Whether to use bootstrap samples when building trees.

Hyperparameter Tuning Random Forest using GridSearchCV and RandomizedSearchCV

Hyperparameter tuning can significantly enhance the performance of Random Forest. Two common methods are:

GridSearchCV:

Explores all possible combinations of hyperparameter values.

Example:

from sklearn.model_selection import GridSearchCV
param_grid = {
    'n_estimators': [100, 200, 300],
    'max_depth': [10, 20, None],
    'min_samples_split': [2, 5, 10]
}
grid_search = GridSearchCV(RandomForestClassifier(), param_grid, cv=5)
grid_search.fit(X_train, y_train)
print(grid_search.best_params_)

RandomizedSearchCV:

Randomly samples a fixed number of hyperparameter combinations.

Example:

from sklearn.model_selection import RandomizedSearchCV
param_dist = {
    'n_estimators': [100, 200, 300],
    'max_depth': [10, 20, None],
    'min_samples_split': [2, 5, 10]
}
random_search = RandomizedSearchCV(RandomForestClassifier(), param_dist, n_iter=10, cv=5)
random_search.fit(X_train, y_train)
print(random_search.best_params_)

OOB Score: Out-of-Bag Evaluation

The Out-of-Bag (OOB) score is an internal validation metric for Random Forest:

How it Works:
- Each tree is trained on a bootstrap sample. The OOB score is computed by testing the tree on samples not included in the bootstrap sample.
Advantages:
- Provides an unbiased estimate of model performance.
- Reduces the need for a separate validation set.

Implementation:

rf = RandomForestClassifier(oob_score=True)
rf.fit(X_train, y_train)
print("OOB Score:", rf.oob_score_)

Feature Importance in Random Forest

Random Forest provides a straightforward way to measure feature importance:

Calculation:
- Measures the decrease in impurity (e.g., Gini index or entropy) caused by a feature across all trees.
Advantages:
- Helps identify the most influential features for predictions.