Momentum and Nesterov Momentum: Accelerating Convergence in Optimization

by
momentum

Momentum: Leveraging Inertia

Training deep learning models often involves minimizing complex, high-dimensional loss functions. Two powerful optimization techniques that enhance convergence are Momentum and Nesterov. These methods smooth updates and accelerate the optimizer’s progress, particularly in challenging optimization landscapes. Let’s delve into how these techniques work and why they’re so effective

it is inspired by the concept of inertia in physics. It improves upon standard gradient descent by considering not only the current gradient but also the previous updates, which helps smooth out oscillations and accelerates convergence.

How it Works

it introduces a velocity term that accumulates past gradients, effectively acting as a memory of recent updates. The update rules for are:

  • Velocity Update: vt+1=βvt−η∇f(θt)
  • Parameter Update: θt+1=θt+vt+1

Where:

  • vt: Velocity term (an exponentially weighted average of gradients).
  • β: Momentum coefficient (typically between 0.8 and 0.99).
  • η: Learning rate.
  • ∇f(θt): Gradient of the loss function.

Key Benefits

  • Smooths Updates: Reduces erratic movements in directions where gradients oscillate, such as in ravines.
  • Speeds Up Convergence: Helps accelerate progress in consistent gradient directions, reducing training time.
  • Handles Noise: Dampens the effect of noisy gradients in stochastic gradient descent (SGD).

it is particularly effective in landscapes with steep valleys and plateaus, as it helps the optimizer glide past such regions faster.

 

Nesterov: Anticipating the Future

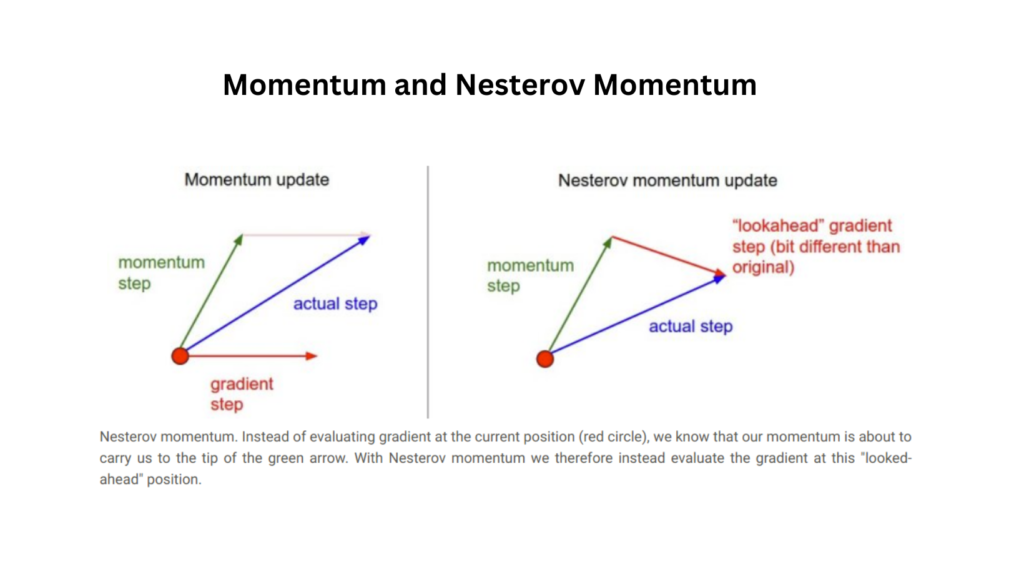
Nesterov Accelerated Gradient (NAG), builds upon standard momentum by introducing a “lookahead” mechanism. This anticipates the future position of the parameters, making updates more informed.

How Nesterov Works

Instead of computing the gradient at the current position, Nesterov evaluates it at a lookahead position:

  1. Lookahead Position: yt=θt+βvt
  2. Velocity Update: vt+1=βvt−η∇f(yt)
  3. Parameter Update: θt+1=θt+vt+1

Key Benefits

  • Sharper Updates: The lookahead mechanism allows for a more accurate adjustment of parameters.
  • Improved Convergence Speed: Nesterov can converge faster than standard, especially in convex and smooth optimization problems.
  • Enhanced Stability: It avoids overshooting and oscillations near optima, ensuring smoother convergence.

Momentum vs. Nesterov

 

FeatureMomentumNesterov 
Gradient CalculationAt the current position.At the lookahead position.
Update MechanismDoes not anticipate future updates.Anticipates future updates.
Convergence SpeedFaster than vanilla gradient descent.Typically faster and more stable.
Handling OscillationsReduces oscillations in gradients.Further minimizes oscillations.

Why Use Momentum Techniques?

Both Momentum and Nesterov offer several advantages over standard gradient descent:

  1. Faster Convergence: They accelerate the optimization process by building on previous updates.
  2. Stability in Complex Landscapes: By smoothing out updates, they effectively handle noisy or fluctuating gradients.
  3. Avoiding Local Minima: They can help the optimizer escape shallow local minima and plateaus.

Practical Considerations

  • Learning Rate (η): Momentum methods require careful tuning of the learning rate to balance convergence speed and stability.
  • Momentum Coefficient (β): A higher value (e.g., 0.9) gives more weight to past gradients, which is useful for smooth surfaces but may slow down in highly variable terrains.
  • When to Use Nesterov: If the loss surface is particularly complex or exhibits steep curvatures, Nesterov  lookahead property can provide a significant edge.

Momentum and Nesterov  are cornerstone techniques in optimization for deep learning. By leveraging past updates, they smooth out erratic movements, accelerate convergence, and improve stability. While standard Momentum is effective in most scenarios, Nesterov adds a predictive step, often leading to faster and more reliable training outcomes.

When tuning your models, experimenting with these methods can lead to significant performance improvements, making them indispensable tools for modern deep learning practitioners.

Frequently Asked Questions (FAQs)

1. What is the main difference between Momentum and Nesterov ?

It calculates gradients at the current position, while Nesterov calculates gradients at a lookahead position. This lookahead feature makes Nesterov  more effective in anticipating parameter updates and reducing overshooting.

2. Why do we need Momentum in optimization?

it helps smooth out updates by accumulating gradients over time, reducing oscillations, and accelerating convergence, especially in scenarios with noisy or oscillating gradients. It is particularly useful in training deep learning models with complex loss surfaces.

3. When should I use Nesterov  instead of standard Momentum?

Use Nesterov when:

  • You want faster convergence.
  • The optimization problem has steep ravines or a highly curved loss surface.
  • You are working on a high-dimensional optimization task where better-informed updates can make a significant difference.

4. What is the typical value for the momentum coefficient (β)?

The momentum coefficient is usually set between 0.8 and 0.99, with 0.9 being a common default. Higher values give more weight to past gradients but may slow updates in highly variable regions.

5. Can Momentum and Nesterov be combined with other optimization algorithms?

Yes, Momentum and Nesterov are commonly integrated with algorithms like Stochastic Gradient Descent (SGD) and sometimes with adaptive methods like Adam or RMSProp.

Leave a Comment