The Central Limit Theorem (CLT) is a fundamental principle in statistics that underpins many of the methods and techniques used in data analysis, machine learning, and scientific research. By explaining how the sample means of independent and identically distributed (i.i.d.) random variables converge to a normal distribution, the CLT provides the foundation for probabilistic inferences about populations based on sample data. In this blog, we will delve into the intricacies of the CLT, explore its conditions, discuss its significance, and illustrate its applications in statistics and machine learning.
What is the Central Limit Theorem (CLT)?
The Central Limit Theorem states that:
The distribution of the sample means of a large number of independent and identically distributed random variables will approach a normal distribution, regardless of the underlying distribution of the variables.
To put it simply, when you repeatedly draw samples from any population (whether the population is normally distributed or not) and calculate their means, those means will form a normal distribution as the sample size increases. This convergence toward a normal distribution is what makes the CLT so powerful.
Key Conditions for the Central Limit Theorem
The CLT does not apply universally; it holds true under specific conditions. Here are the main requirements:
Sample Size: The sample size must be sufficiently large. A commonly accepted rule of thumb is that the sample size should be 30 or more. However, this number can vary depending on the skewness of the population distribution; more skewed distributions may require larger sample sizes.
Finite Variance: The population from which the samples are drawn must have a finite variance. If the population variance is infinite, the CLT does not apply.
Independence and Identical Distribution: The random variables in the sample must be independent and identically distributed (i.i.d.). This means each random variable must be drawn independently from the same probability distribution.
Why is the Central Limit Theorem Important?
The CLT is significant for several reasons, especially in the fields of statistics and machine learning:
Facilitating Inferences About Populations:
The CLT enables us to estimate population parameters, such as the mean, using sample data. This is crucial in situations where analyzing the entire population is impractical.
Foundation for Hypothesis Testing:
Techniques like t-tests and ANOVA rely on the CLT to determine whether observed differences between groups are statistically significant.
Confidence Intervals:
By knowing that sample means follow a normal distribution, we can construct confidence intervals to estimate population means with a specific level of confidence.
Simplifying Complex Distributions:
Regardless of the underlying population distribution, the CLT allows us to work with the normal distribution when analyzing sample means, simplifying calculations and interpretations.
Application in Machine Learning:
Many machine learning algorithms assume normality in their underlying data distribution. The CLT justifies these assumptions when the data consists of aggregated samples.
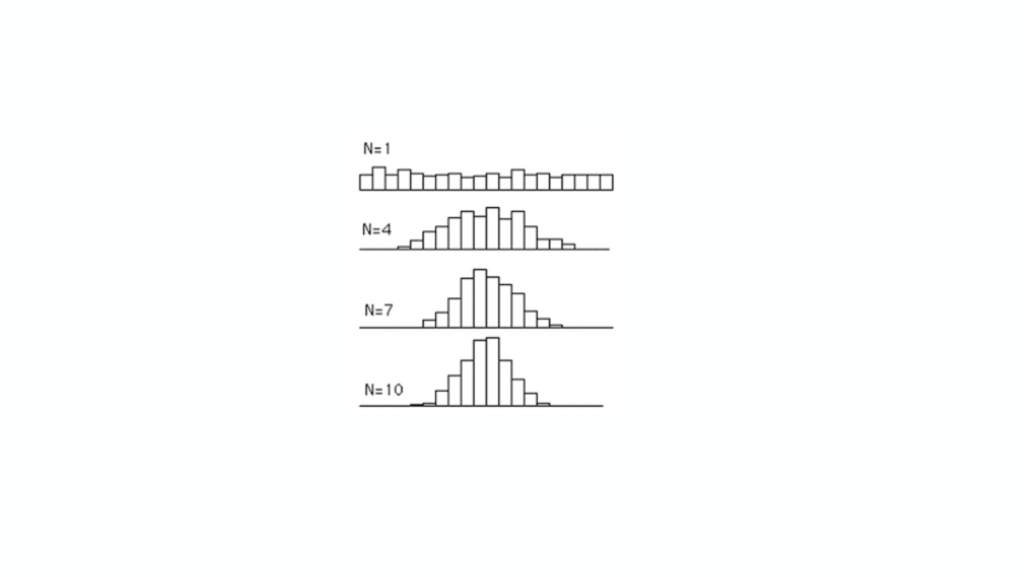
Visualizing the Central Limit Theorem
To better understand the CLT, let’s consider a practical example:
Example: Rolling a Die
Imagine rolling a six-sided die multiple times. The outcomes (1, 2, 3, 4, 5, 6) are uniformly distributed—each number has an equal probability of appearing. If we take a single roll, the distribution of outcomes is uniform, not normal.
Now, suppose we roll the die 30 times, calculate the average of the outcomes for each trial, and repeat this process 1,000 times. The histogram of these sample means will form a bell-shaped curve, resembling a normal distribution. This transformation occurs because of the Central Limit Theorem.
Applications of the Central Limit Theorem
The practical implications of the CLT extend across numerous domains. Let’s explore its applications in detail:
1. Statistical Inference
Confidence Intervals: The CLT allows us to construct confidence intervals for population means. For instance, in survey analysis, we can estimate the average income of a population based on a sample of respondents.
Hypothesis Testing: When testing a hypothesis, such as comparing the effectiveness of two treatments, the CLT ensures the validity of test statistics that rely on the normal distribution.
2. Quality Control
In manufacturing, the CLT is used to monitor production processes. By sampling and analyzing a subset of items, engineers can infer the overall quality of a production batch.
3. Financial Modeling
In finance, the CLT underpins models for stock price movements and portfolio returns, which often involve aggregated data over time or across assets.
4. Machine Learning and AI
Feature Normalization: Many algorithms, such as Support Vector Machines (SVM) and Neural Networks, assume normally distributed input features. The CLT helps justify feature scaling and normalization techniques.
Ensemble Methods: Techniques like bagging and boosting rely on aggregating predictions from multiple models. The aggregated predictions often approximate a normal distribution due to the CLT.
5. Epidemiology and Public Health
In public health studies, the CLT is used to analyze sample data for estimating population parameters such as disease prevalence and treatment effectiveness.
Mathematical Formulation of the Central Limit Theorem
Let’s dive into the mathematical representation of the CLT:
If are i.i.d. random variables with mean μ and variance σ^2, the sample mean is given by:
The CLT states that as :
Where denotes convergence in distribution, and represents a normal distribution with mean 0 and variance σ^2.
Limitations of the Central Limit Theorem
While the CLT is powerful, it is essential to recognize its limitations:
Non-i.i.d. Data: The CLT does not hold if the data points are not independent or not identically distributed.
Small Sample Sizes: For small sample sizes, the approximation to normality may not be accurate, especially for skewed or heavy-tailed distributions.
Infinite Variance: The CLT is invalid for populations with infinite variance, such as those following a Cauchy distribution.
Practical Tips for Using the CLT
Check Independence: Ensure that the data points in your sample are independent. Correlated data may require different statistical approaches.
Sufficient Sample Size: Use a sufficiently large sample size, particularly when dealing with skewed populations.
Understand Your Data: Be aware of the underlying distribution of your data and the assumptions made by statistical methods.
Leverage Software: Modern statistical software can simulate the CLT for specific scenarios, helping you visualize and understand its implications.
The Central Limit Theorem is a cornerstone of statistics and machine learning, providing the theoretical foundation for many analytical techniques. By understanding and applying the CLT, we can make informed decisions based on sample data, construct robust models, and draw meaningful insights from complex datasets. Whether you are a data scientist, statistician, or researcher, mastering the CLT is essential for unlocking the full potential of statistical analysis.
If you found this explanation helpful, feel free to share it and explore other topics in statistics and machine learning on our blog!